5.8. ZGate#

This gate is popular since it reverses the relative phase.

API References: ZGate

5.8.1. Definition#

Transformation

\[ Z |0\rangle = |0\rangle, \qquad Z |1\rangle = -|1\rangle \]

\(Z\) gate preserves \(|0\rangle\) but flips the phase of \(|1\rangle\). This is a phase gate with prefixed phase change, “-1”.

U gate expression

(5.9)#\[ Z = U\left(0,\frac{\pi}{2},\frac{\pi}{2}\right) \]

R gate expression

\[ z = i R_z(\pi) \]

The Qiskit circuit code symbol is z and it appears in quantum circuit as

from qiskit import QuantumCircuit
qc=QuantumCircuit(1)
qc.z(0)
qc.draw('mpl')
../_images/z_3_0.png

or

qc.draw()

   ┌───┐
q: ┤ Z ├
   └───┘

5.8.2. Acting on a superposition state#

When ZGate is applied to a super position state the relative phase changes by \(\pi\). That is

(5.10)#\[ Z \left (c_0 |0\rangle + c_1 |1\rangle\right) = c_0 |0\rangle - c_1 |1\rangle) \]

In Bloch sphere representation,

\[ Z \left( \cos(\theta/2)|0\rangle + \sin(\theta/2) e^{i\phi}|1\rangle\right) = \cos(\theta/2) |0\rangle + \sin(\theta/2) e^{i (\phi+\pi)} |1\rangle \]

This suggests that the Bloch vector rotates around \(z\) axis by \(\pi\).

Exercise 5.8.1  Show that \(Z|+\rangle = |-\rangle\) and \(Z|-\rangle = |+\rangle\). ZGate flips \(|\pm\rangle\) exactly (YGate flips only up to the global phase). This property is useful in quantum computation.

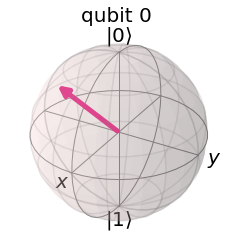
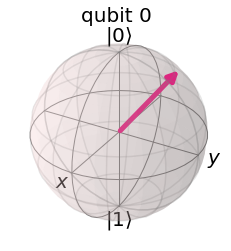
Qiskit Example 5.8.1  Let us demonstrate the effect of ZGate using Qiskit. Using the BLoch sphere representation, ZGate transform \((\theta,\phi)\) to \((\theta,\phi+\pi)\). Try \(\theta=\pi/4\) and \(\phi=-\pi/4\). Check that he Bloch vector rotates around \(z\) axis by \(\pi\).

# import QuatumCircuit and QuantumRegister classes.
from qiskit import QuantumCircuit, QuantumRegister
from qiskit.opflow import Zero, One

# import STatevector class
from qiskit.quantum_info import Statevector

# import numpy
import numpy as np

theta=np.pi/4
phi=-np.pi/4

ket0=np.cos(theta/2)*Zero + np.sin(theta/2)*np.exp(phi*1j)*One

# Preparation
qr=QuantumRegister(1,'q') # create a single qubit with name 'q'.
qc=QuantumCircuit(qr)  # create a quantum circuit

# set the qubit to |L> 
qc.initialize(ket0.to_matrix())

# apply Xgate
qc.z(0)

# Final state
ket1=Statevector(qc)

# Compare the final state with |R> in Bloch sphere.
from qiskit.visualization import plot_bloch_multivector

# Generate Bloch vectors
bloch0 = plot_bloch_multivector(ket0)
bloch1 = plot_bloch_multivector(ket1)

from IPython.display import display

# Compare |psi> and Z|psi>.  They are equivalent in the Bloch sphere.
display("Original |psi>",bloch0,"Z|psi>",bloch1)

'Original |psi>'
../_images/z_9_1.png 
'Z|psi>'
../_images/z_9_3.png

When ZGate acts on a superposition state in \(\{|+\rangle,|-\rangle\}\), what will be the outcome?

5.8.3. Important Properties#

\(Z^2 = I\)

This means that

  1. \(Z^2\) does not do any thing on the qubit.

  2. \(Z\) is self-inverse, that is \(Z^{-1} = Z\).

  3. \(Z\) is self-adjoint (\(Z^\dagger = Z\)) since \(Z\) is unitary (\(Z^\dagger = Z^{-1}\)) by definition.

Last modified: 08/31/2022