5.4. U Gate

When a gate acts on a qubit, it rotates the Bloch vector. Any rotation can be specified with three angles, \(\theta\), \(\phi\), and \(\lambda\). They are known as Euler angles. In standard quantum computation, a standard Euler rotation \(z-y-z\) is used. That is rotating 1) around \(z\) axis by \(\lambda\), 2) around \(y\) axis by \(\theta\), and 3) around \(z\) axis by \(\phi\). The rotations must be done in this order. This gate transforms \(|0\rangle\) to a general qubit state.

Qiskit API References: UGate

5.4.1. Definition

Transformation

\[\begin{split} \begin{eqnarray} U(\theta,\phi,\lambda) |0\rangle &=& \cos(\theta/2) |0\rangle + \sin(\theta/2) e^{i \phi} |1\rangle \\ U(\theta,\phi,\lambda) |1\rangle &=& - e^{i \phi} \left[\sin(\theta/2) |0\rangle - \cos(\theta/2) e^{i \lambda}|1\rangle\right] \end{eqnarray} \end{split}\]

Notice that when it acts on \(|0\rangle\), we obtain a general state in the Bloch sphere expression (4.4) (no \(\lambda\) appears in it).

Matrix expression

\[\begin{split} U(\theta,\phi,\lambda) \doteq \begin{bmatrix} \cos(\theta/2) & - e^{i \phi} \sin(\theta/2) \\ e^{i \lambda} \sin(\theta/2) & e^{i (\lambda+\phi)} \cos(\theta/2)\end{bmatrix} \end{split}\]

Using Rotation gates

The \(U\) gate used to be defined as \(U(\theta,\phi,\lambda)=R_z(\phi) R_y(\theta) R_z(\lambda)\). (See OpenQASM 2.) However, it adds a global phase on the Bloch sphere expression. To remove the inconvenience, now it is officially defined in OpenQASM 3 as

\[ U(\theta,\phi,\lambda) = e^{i (\lambda+\phi)/2} R_z(\phi) R_y(\theta) R_z(\lambda) . \]

The Qiskit circuit code symbol is u and it appears in quantum circuit as

from qiskit.circuit import QuantumCircuit, Parameter
theta=Parameter('\u03B8')
phi=Parameter('\u03D5')
lamb=Parameter('\u03BB')
qc=QuantumCircuit(1)
qc.u(theta,phi,lamb,0)
qc.draw('mpl')

or

qc.draw()

   ┌──────────┐
q: ┤ U(θ,ϕ,λ) ├
   └──────────┘

---

Qiskit Example 5.4.1  Generate a state \(\cos(\pi/3)|0\rangle + \sin(\pi/3) e^{-i \pi/7} |1\rangle\) in a quantum circuit.

# import numpy
import numpy as np

# import QuatumCircuit and QuantumRegister classes.
from qiskit import QuantumCircuit, QuantumRegister

# import STatevector class
from qiskit.quantum_info import Statevector

# Preparation
qr=QuantumRegister(1,'q') # create a single qubit with name 'q'.
qc=QuantumCircuit(qr)  # create a quantum circuit

#  apply the Ugate to the qubit
qc.u(np.pi/5,-np.pi/3,0,0)

# Plot the final state
Statevector(qc).draw('bloch')

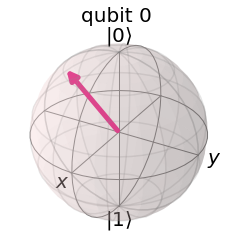
5.4.2. Acting on a superposition state

\[ U(\theta,\phi,\lambda)\left(c_0|0\rangle+c_1|1\rangle\right) =\left[c_0 \cos(\theta/2) - c_1 e^{i\phi} \sin(\theta/2)\right]|0\rangle + e^{i \phi} \left[ c_0 \sin(\theta/2) + c_1 e^{i \lambda}\cos(\theta/2) \right]|1\rangle \]

---

Last modified: 08/31/2022