5.12. P Gate#

P gate is also known as phase gate. This gate contains a parameter.

API References: PhaseGate

5.12.1. Definition#

Transformation

\[\begin{split} \begin{align} &P(\theta) |0\rangle = |0\rangle, && P(\theta) |1\rangle = e^{i \theta}|1\rangle\\ &P^\dagger(\theta) |0\rangle = |0\rangle, && P^\dagger(\theta) |1\rangle = e^{-i \theta}|1\rangle \end{align} \end{split}\]

Matrix expression

\[\begin{split} P(\theta) = \begin{bmatrix}1&0\\0&e^{i \theta}\end{bmatrix}, \qquad P^\dagger(\theta) = \begin{bmatrix}1&0\\0&e^{-i \theta}\end{bmatrix} \end{split}\]

U gate expression

\[ P = U\left(0,0,\theta \right) = U\left(0,\theta,0 \right), \quad P^\dagger = U\left(0,0,-\theta\right)= U\left(0,-\theta,0\right) \]

R gate expression

\[ P = e^{i \theta/2} R_z(\theta), \quad P^\dagger = e^{-i \theta/2} R_z(-\theta) \]

The qiskit circuit symbol is p. It appears in quantum circuits as

from qiskit.circuit import QuantumCircuit, Parameter
t=Parameter('\u03B8')
qc=QuantumCircuit(1)
qc.p(t,0)
qc.draw('mpl')
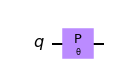
../_images/p_2_0.png

or

qc.draw()

   ┌──────┐
q: ┤ P(θ) ├
   └──────┘

\(Z\), \(S\), \(T\) and \(P\) all rotates the Bloch vector around the \(z\) axis. gates are special cases of \(P\) gate: \(Z=P(\pi)\), \(S=P(\pi/2)\) and \(T=P(\pi/4)\). While these relations are mathematically exact and \(P\) gate can replace them, the parameter-free gates should be used when the rotation angle

5.12.2. Acting on a superposition state#

When PGate is applied to a superposition state, the coefficient to \(|0\rangle\) remains the same but that of \(|1\rangle\) gets additional phase factor. That is

(5.29)#\[ P(t) \left (c_0 |0\rangle + c_1 |1\rangle\right) = c_0 |0\rangle + e^{it} c_1 |1\rangle \]

In Bloch sphere representation,

\[ P(t) \left( \cos(\theta/2)|0\rangle + \sin(\theta/2) e^{i\phi}|1\rangle\right) = \cos(\theta/2) |0\rangle + \sin(\theta/2) e^{i (\phi+t)} |1\rangle \]

This suggests that the Bloch vector rotates around \(z\) axis by \(t\).

Last modified: 08/31/2022