5.14. State tomography#

State tomography is an experimental method to determine the state of a quantum system. In this section, we try to determine the pure state of a qubit by quantum computation. Measurement of a single qubit cannot determine it due to the stochastic nature of quantum measurement. We must prepare many qubits in the same state.

In Section 5.13.2, we developed a quantum circuit that determines the quantum phase of a qubit. In that example, we had only one parameter, \(\phi\), to be determined. To obtain the full information (up to the global phase) of the state vector, we have to determine two parameters. Recall that the state of a qubit can be expressed as

\[ |\psi\rangle = \cos\left(\frac{\theta}{2}\right) |0\rangle + \sin\left(\frac{\theta}{2}\right) e^{i \phi}|1\rangle \]

Measuring this state directly, we obtain only \(\left|\cos\left(\frac{\theta}{2}\right)\right|\) and \(\left|\sin\left(\frac{\theta}{2}\right)\right|\). Neither \(\theta\) nor \(\phi\) can be determined from them. We need a quantum algorithm similar to the method used in Section 5.13.2. See the following Strategy box on State Tomography.

5.14.1. Algorithm#

To determine the Bloch vector corresponding to a pure state \(\psi\rangle\), change the \(x\)-, \(y\)-, \(z\)-basis to the computational basis and measure the state in the computational basis.

  • \(x\) component
    Change the basis from the \(x\)-basis to the computational basis by the \(H\) gate.
    Measure \(H |\psi\rangle\). Then, \(r_x = \sin\theta \cos \phi = p_0 -p_1\).

  • \(y\) component
    Change the basis from the \(y\)-basis to the computational basis by the \(H\cdot S^\dagger\) gate.
    Measure \((H\cdot S^\dagger) |\psi\rangle\). Then, \(r_y = \sin\theta \sin\phi = p_0 -p_1\).

  • \(z\) component
    Since the \(z\)-basis and the computational basis are the same, no need to change the basis.
    Measure \(|\psi\rangle\). Then, \(r_z = \cos\theta = p_0 -p_1\).

One the Bloch vector is measured, we can calculate the angles by \(\theta = \text{arccos}(r_z)\) and \(\phi = \text{arctan2}.(r_y,r_x)\).

This method relies on the probabilities of finding |0> and |1>. In order to get an accurate result, we need a sufficient number of samplings. Hence, we must run the circuit many times.

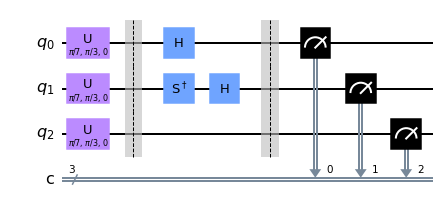
5.14.2. Circuit#

import numpy as np

from qiskit import *

# two classical registers
cr=ClassicalRegister(3,'c')

# two quantum registers (qubits)
qr=QuantumRegister(3,'q')

# set the quantum circuit
qc=QuantumCircuit(qr,cr)

# set parameters
theta=np.pi/7
phi=np.pi/3

# Generation of the state
qc.u(theta,phi,0,[0,1,2])

# separate the preparation part from the phase determination
# by placing a barrier
qc.barrier([0,1,2])

# x-component
qc.h(0)

# y-component
qc.sdg(1)
qc.h(1)

qc.barrier()

# measure the both qubits
qc.measure(qr,cr)

# show the circuit
qc.draw('mpl')
../_images/tomography_3_0.png

5.14.3. Execution#

# noisy or noiseless simulation
noise=True

# Chose a quantum simulator
if noise:
    # Using Fake IBM Jakarta
    from qiskit.providers.fake_provider import FakeJakarta
    backend = FakeJakarta()
    print("noise is on: Using FakeJakarta")
else:
    # Using noiseless simulator
    backend = Aer.get_backend('qasm_simulator')
    print("noise is off:  Using Qasm_simulatior.")

# set the number of tries
nshots=8192

# execute the quantum circuit and store the outcome
job = backend.run(qc,shots=nshots)

# extract the result
result = job.result()

# count the outcome
counts = result.get_counts()

from qiskit.result import marginal_counts

# marginal counts of each component
counts_x = marginal_counts(result,indices=[0]).get_counts()
counts_y = marginal_counts(result,indices=[1]).get_counts()
counts_z = marginal_counts(result,indices=[2]).get_counts()

# get the Bloch vector components
rx=(counts_x['0']-counts_x['1'])/nshots
ry=(counts_y['0']-counts_y['1'])/nshots
rz=(counts_z['0']-counts_z['1'])/nshots

# evaluate the phase angle
theta_qc=np.arccos(rz)
phi_qc=np.arctan2(ry,rx)


# print out the results
print("measured   phi = {:6.3f} (exact  = {:6.3f} )".format(phi_qc, phi))
print("measured theta = {:6.3f} (exact  = {:6.3f} )".format(theta_qc,theta))

noise is on: Using FakeJakarta
measured   phi =  0.982 (exact  =  1.047 )
measured theta =  0.478 (exact  =  0.449 )

Last modified: 08/31/2022