5.3.2. Improper Integrals II: Integrable Singularities

Consider integral

(5.8)\[ \int_0^1 \frac{1}{\sqrt{x}} dx = 2. \]

The integrand diverges at \(x=0\) but the integral is finite. This is a kind of improper integral ubiquitous in physics.

How can we calculate this type of integrals numerically? The methods we developed in the previous section are not applicable for this type of integrals due to divided-by-zero error.

In this section we discuss two commonly used methods: one based on variable transformation and the other on the isolation of singularity.

5.3.2.1. The method of variable transformation

Let us consider a simple example:

(5.9)\[ \int_0^1 \frac{1}{(1+x)\sqrt{x}} dx = \frac{\pi}{2} \]

The integrand at \(x=0\) diverges and thus the direct application of the previous methods fails. Generally, such integrable singularity can be eliminated by variable transformation. Let \(y=\sqrt{x}\). Then \(dy = \displaystyle \frac{2}{\sqrt{x}} dx\). Substituting this in the original integral, we obtain

(5.10)\[ \int_0^1 \frac{2}{y^2+1} dy \]

which contains no singularity. The methods of piece-wise integration work fine.

Now we verify numerically that integral (5.10) agrees with the original integral. The agreement with the exact answer is very good.

import numpy as np

# We use the Simpson rule
from scipy.integrate import simpson

# number of sampling points
N = 100

# evaluation points
y=np.linspace(0,1,N)

# integrand
f =2/(y**2+1)

# integrate using simpson in scipy
numerical = simpson(f,x=y)
analytical = np.pi/2
error = numerical - analytical
print(" numerical =",numerical)
print("analytical =",analytical)
print("     error =",error)

 numerical = 1.5707963268218346
analytical = 1.5707963267948966
     error = 2.6938007380294948e-11

In general the following form of improper integrals can be transformed by variable transformation \(y=x^p\):

(5.11)\[ \int_0^1 \frac{f(x)}{x^p} dx = \frac{1}{p} \int_0^1 f(y^{1/p}) y^{1-2p} dy \]

where \(0 < p \le \frac{1}{2}\) and \(f(x)\) is analytic in interval \([0,1]\).

---

Exercise 5.3.2.1

Verify the following integral using a numerical method. $\( \int_0^1 \frac{x^{-1/3}}{(x^2+1)} dx = \frac{1}{6}(\sqrt{3} \pi + \ln 3) \)$

---

In practical applications, the form of singularity is not clearly visible. For example, consider

\[ \int_0^{\pi/2} \frac{1}{\sqrt{\sin x}} dx = \sqrt{2} K\left(\frac{1}{2}\right) \approx 2.622057554 \]

where \(K(x)\) is the complete elliptic integral of the first kind. Since \(\sin(0)=0\), there is a singularity at \(x=0\). However, the integral is finite. Hence, there must be an integrable singularity. Using the power series of the sine function \(\sin(x) = x - \frac{x^3}{3!} + \cdots\), we find that \(\sqrt{\sin{x}} \sim \sqrt{x}\) in the vicinity of \(x=0\). By multiplying and dividing the integrand by \(\sqrt{x}\) the integral can be expressed as

\[ \int_0^{\pi/2} \left(\frac{\sqrt{x}}{\sqrt{\sin x}}\right) \frac{1}{\sqrt{x}} dx . \]

Note that there is no sigularity inside the parenthesis since

\[ \lim_{x\rightarrow 0} \frac{\sqrt{x}}{\sqrt{\sin x}} = 1 \]

Now, we use the trick of variable transformation \(y=\sqrt{x}\), and the integral becomes

\[ \int_0^{\sqrt{\pi/2}} \frac{2 y}{\sqrt{\sin y^2}} dy \]

which has no singularity. Mathematically speaking the singularity is removed but computationally the divide-by-zero issue remains. We need to evaluate the integrand at \(y=0\) by taking limit

\[ \lim_{y\rightarrow 0} \frac{2y}{\sqrt{\sin y^2}} = 2 \]

Now we are ready to compute the integral.

import numpy as np
from scipy.integrate import simpson

# complete elliptic integral of the first kind in scipy
from scipy.special import ellipk

# number of sampling points
N = 100

# evaluation points
y=np.linspace(0,1,N)*np.sqrt(np.pi/2)

# to avoild devided-by-zero error, y=0 is temporarily replaced with 1
y[0]=1

f=2*y/np.sqrt(np.sin(y**2))

# recover y=0
y[0]=0

# to avoid devided-by-zero error, manually enter the integrand at y=0
f[0]=2

# integration using simpson
numerical = simpson(f,x=y)

# exact integral
elliptic = np.sqrt(2)*ellipk(0.5)

print(" numerical =", numerical)
print("  elliptic =", elliptic)
print("     error =", numerical-elliptic)

 numerical = 2.6220575968235917
  elliptic = 2.62205755429212
     error = 4.253147167787574e-08

The agreement between the exact and numerical result is very good.

Algorithm 5.1: Integrable Singularity I

:name: integrable-singularity-1

Integral

\[ \int_a^b F(x) dx. \]

where \(F(x)\) has an integrable singularity at \(x=a\), can be transformed to a singularity-free integral by the following procedures.

1. Inspect the integrand near \(x=0\) and find the type of singularity: \(F(x) \sim \displaystyle\frac{A}{(x-a)^p}\) where \(0<p<\frac{1}{2}\) and \(A\) is a constant.

2. Rewrite the integral as

\[ \int_a^b \frac{f(x)}{(x-a)^p} dx. \]

where \(f(x) = F(x) (x-a)^p\).

3. Using variable transformation \(y=(x-a)^p\), the integral is transformed to [see Eq. (5.11)]

(5.12)\[ \frac{1}{p} \int_0^{(b-a)^p} f(y^{1/p}+a) y^{1-2p} dy = \frac{1}{p} \int_0^{(b-a)^p} F(y^{1/p}+a) y^{2(1-p)} dy \]

4. Evaluate the new integrand at \(y=0\) by taking limit

\[\begin{split} \lim_{y\rightarrow 0} \frac{1}{p} F(y^{1/p}+a) y^{2(1-p)} = \lim_{y\rightarrow 0} \frac{A}{p} y^{1-2p} = \begin{cases} 0 & p < 1/2 \\ 2A & p=1/2\end{cases} \end{split}\]

5. Evaluate the integral (5.12) using a standard numerical integration method.

5.3.2.2. The method of singularity isolation

The method of variable transformation is useful for most cases. There is another method which may be simpler in some cases.

Consider the improper integral (5.9) again. The integrand in the visicinity of \(x=0\) is \(1/\sqrt{x}\) as discussed in the above. We can remove the singularity from the integrand as

\[ f(x) = \frac{1}{(1+x)\sqrt{x}} - \frac{1}{\sqrt{x}} \]

Notice that \(f(x)\) is not singular at $x=0. Since the singular part can be analytically integrated as given in Eq. (5.8),
the original integral (5.9) is expressed as

(5.13)\[ \int_0^1 \frac{1}{(1+x)\sqrt{x}} dx = \int_0^1 f(x) dx + 2 \]

The integral in the right hand side can be integrated by a standard numerical method. Unlike the variable transformation method, there is no divided-by-zero issue since \(f(0)=0\). This approach is simpler than the variable transformation from the numerical calculation point of view, particularly when the integrand takes a mathematically complicated form.

Before evaluation the above integral, we visually check the new integrand.

import numpy as np
import matplotlib.pyplot as plt

N=100

# evaluation points. x=0 is excluded.
x=np.linspace(0.01,1,N)

f0=1/np.sqrt(x)
f1=1/(1+x)/np.sqrt(x)
f2=f1-f0

plt.figure(figsize=(5,4))
plt.plot(x,f1,'-k',label="original integrand")
plt.plot(x,f0,'--r',label="singular part")
plt.plot(x,f2,'-b',label="non-singular part")
plt.axhline(y = 0, color = '0.8', linestyle = '-')
plt.legend(loc=1)
plt.show()

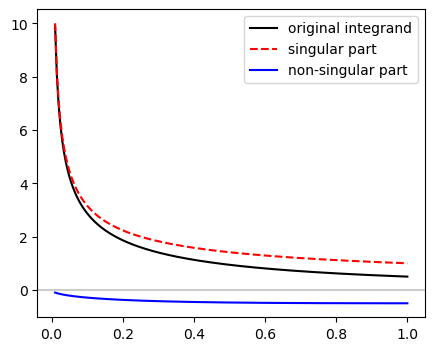
The black line shows the original integrand (5.9) and the red dashed line is the singular part. The two curves coincide near \(x=0\). The difference between them (the blue line) is finite and smooth. It seems easy to integrate it numerically with a piecewise integration method.

Now, we evaluate the integral. The singular part is analytically integrated and added to the numerical integration of the non-singular part.

import numpy as np
from scipy.integrate import simpson

N=201

# evaluation points
x=np.linspace(0,1,N)

# to avoild devided-by-zero error, x=0 is temporarily replaced with 1
x[0]=1

f=1/(1+x)/np.sqrt(x) - 1/np.sqrt(x)

# recover x=0
x[0]=0

# the integrand at x=0 is 0 always
f[0]=0

# integrate using the Simpson rule
s = simpson(f,x=x)

# add the singular part
numerical=s+2
# exact value
analytical=np.pi/2

print("     Numerical =",numerical)
print("    Analytical =",analytical)
print("         Error =",numerical-analytical)

     Numerical = 1.5708250549553062
    Analytical = 1.5707963267948966
         Error = 2.8728160409663417e-05

The error is not as small as that of the variable transformation method.

Algorithm 5.2: Integrable Singularity II

:name: integrable-singularity-2

Integral

\[ \int_a^b F(x) dx. \]

where \(F(x)\) has an integrable singularity at \(x=a\), can be transformed to a singularity-free integral by the following procedures.

1. Inspect the integrand near \(x=0\) and find the type of singularity: \(F(x) \sim \displaystyle\frac{A}{(x-a)^p}\) where \(0<p<\frac{1}{2}\) and \(A\) is a constant.

2. Introduce singularity free integrand as

\[ f(x) = F(x) - \frac{A}{(x-a)^p} \]

3. Numerically calculate integral

\[ I = \int_a^b f(x) dx \]

4. Calculate the original integral by adding back the singular part

\[ \int_a^b F(x) dx = \int_a^b f(x) dx + \int_a^b \frac{A}{(x-a)^p} dx = I + \frac{A (b-a)^{1-p}}{1-p} \]

---

Example 5.3.2.1

Evaluate \(\displaystyle\int_{-1}^{1} \frac{P_n(x)}{\sqrt{1-x}} dx \) where \(P_n(x)\) is the Legendre polynomial of degree \(n\). The exact answer is known to be \(\displaystyle\frac{2\sqrt{2}}{2n+1}\).

At \(x=1\), the integrand is \(\frac{P_n(1)}{\sqrt{1-x}}\). Since \(P_n(1)=1\), there is a singularity at \(x=1\). The singular part can be integrated as \(\displaystyle\int_{-1}^{1} \frac{P_n(1)}{\sqrt{1-x}} dx = 2 \sqrt{2} P_n(1)\). We evaulate the non-singular part,

\[ \int_{-1}^{1} \frac{P_n(x) - P_n(1)}{\sqrt{1-x}} dx \]

using the Simpson rule. The following code uses simpson and legendre in the scipy package.

import numpy as np
from scipy.integrate import simpson
from scipy.special import legendre

# choose the degree of the polynomial
n=2

# define the Legendre polynomial
P=legendre(n)

N=201
x=np.linspace(-1,1,N)

# avoid x=1
x[N-1]=0

# construct singularity free integrand
f=(P(x)-P(1))/np.sqrt(1-x)

# recover x=0
x[N-1]=1

# the integrand at x=1 is 0
f[N-1]=0

s=simpson(f,x=x)

# adding the singular part back
numerical=s+2*np.sqrt(2)*P(1)
analytical=2*np.sqrt(2)/(2*n+1)

print("     Numerical =",numerical)
print("    Analytical =",analytical)
print("         Error =",numerical-analytical)

     Numerical = 0.5659291899157886
    Analytical = 0.565685424949238
         Error = 0.00024376496655054147

The agreement with the theory is not bad.

---

Exercise 5.3.2.1

Evaluate the integral using the method of variable transformation and compare the accuracy with the above calculation.

---

Last updated: Aug 23, 2025