2.3.2. Quantum Free Falling

Consider a classical particle of mass \(m\) is freely falling under the constant gravity \(g\). At time \(t=0\), the particle was located at the height \(z=0\) with zero velocity \(v=0\). The position of the particle at time \(t\) is \(z(t) = - \frac{1}{2} g t^2\) and its velocity is \(v(t) = - g t\) as we learned in a freshman physics course. Both the gravitational potential energy and the kinetic energy are initially zero, thus the total energy remains zero due to the conservation of energy.

Now,we consider a quantum particle in the same situation. The corresponding Schr\(\"{o}\)dinger equation is

\[ \left(-\frac{hbar^2}{2m} \frac{d^2}{dz^2} + m g z \right) \psi(z) = E \psi(z) \]

Since the energy is zero, the equation to be solved is

\[ \left(-\frac{hbar^2}{2m} \frac{d^2}{dz^2} + m g z \right) \psi(z) = 0 \]

Since the particle is falling, the wavefunction should vanish as \(z \rightarrow \infty\). The solution can be written as follows:

\[ \psi(z) = \text{Ai} \left [ \left ( \frac{2m^2g}{\hbar^2} \right )^{1/3} z \right ] \]

where \(\text{Ai}(x)\) is the Airy function which is a solution to the diffferential equation \(y'' - x y = 0\). `

While we obtained an exact solution in a closed mathematical form, we don’t know how it behaves without the knowledge of the Airy function. Let us plot the wavefunction and see if the solution make a sense. We use a normalized coordinate \(\xi = \left ( \frac{2m^2g}{\hbar^2} \right )^{1/3} z\).

Scipy contains the Airy function but it returns 4 functions, the first and second kinds of the Airy function, Ai and Bi, and their derivatives. We need only Ai which is the first function returned by scipy.special.airy. Whenever we use a canned routine, we must check the usage carefully. See the documentation.

import numpy as np
from scipy.special import airy
import matplotlib.pyplot as plt

# 401 evaluation points between -15 and 5
xi = np.linspace(-15,5,401)
psi = airy(xi)[0]

plt.plot(xi,psi)
plt.xlabel(r"$\xi$")
plt.ylabel(r"$\psi(\xi)$")
plt.axhline(y = 0.0, color = 'k', linestyle = '--') 
plt.show()

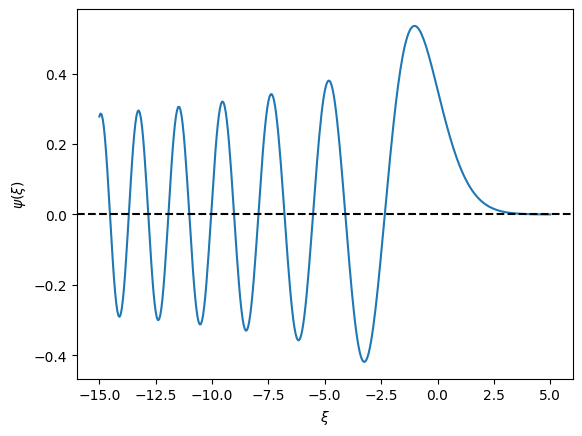
First of all, we notice that the wavefunction oscillates below \(z=0\), indicating that the particle is moving almost freely. Recall that the wavefunction of a free particle is \(\cos(k z)\) and \(\sin(k z)\). Secondly, the wavelength becomes shorter and shorter as \(z\) decreases, meaning that the momentum is getting larger and larger. It consistents with the classical falling particle.

We also notice that the wavefunction does not vanish above \(z=0\). Strangely, the quantum particle can be observed above the starting point. The classical particle won’t moves up by itself against the gravity. It is seemingly violating the conservation of energy, unless the kinetic energy gets negative. This is one of the strange quantum phenomena that commonly appear for a quantum particle trapped in a potential well.[3] This is also closely related to the quantum tunneling.

---

Last modified on 3/9/2024 by R. Kawai.