2.2. Plotting functions

Visualization of functions help understanding the mathematical expression. Here we plot various functions using matplotlib package.

2.2.1. A Simple Plot

A simple way to plot a function is to express the function as an array First we generate points \(\{x_1, \cdots, x_N\}\) where the function is evaluated. Store the function as array \(\{f(x_i), \cdots, f(x_N)\}\). We utilize numpy module, linspace to generate grid points.

import numpy as np
import matplotlib.pyplot as plt

# generates 101 points between 0 and 15 
x = np.linspace(0,15,101)

# evaluate the function at each point
f = np.cos(x)

# plot it using the default options.
plt.plot(x,f)
plt.xlabel("x")
plt.ylabel("f(x)")

Text(0, 0.5, 'f(x)')

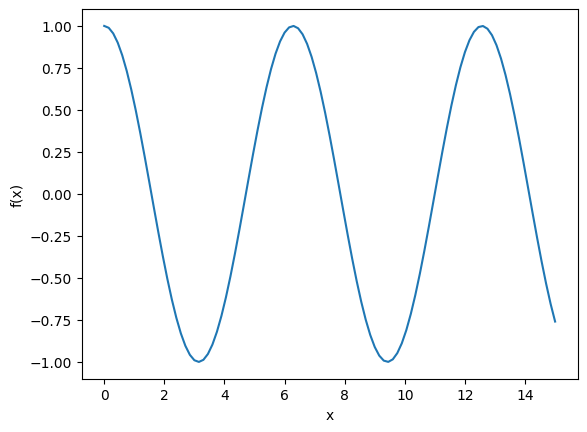
2.2.2. Multiple plots

We can plot multiple curves in the same graph with different colors and types of lines.

# plot with various options

g = np.sin(x)

# set the canvas size
plt.figure(figsize=(5,3))

# black solid line with label
plt.plot(x,f,'-k',label=r"$cos(x)$")

# red dashed line with label
plt.plot(x,g,'--r',label=r"$sin(x)$")

plt.xlabel("x")
plt.ylabel("f(x)")

# show the labels as legend
plt.legend(loc=0)

<matplotlib.legend.Legend at 0x7efc611ac9d0>

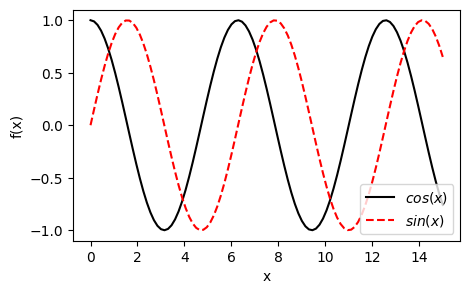
Exercise: Plot \(f(x)=x \cos(x)\) and \(g(x) =x \sin(x)\) in the same graph, one with a blue solid line and the other with a green dashed line..

2.2.3. Multiple graphs

You can plot curves in two different graphs.

plt.ioff()
plt.figure(figsize=(10,3))

# plot in the left panel
plt.subplot(1,2,1)
# blue solid line with label
plt.plot(x,f,'-b',label=r"$cos(x)$")
plt.xlabel("x")
plt.ylabel("f(x)")

plt.subplot(1,2,2)
plt.plot(x,f,'*r',label=r"$sin(x)$")
plt.xlabel("x")
plt.ylabel("f(x)")

plt.show()

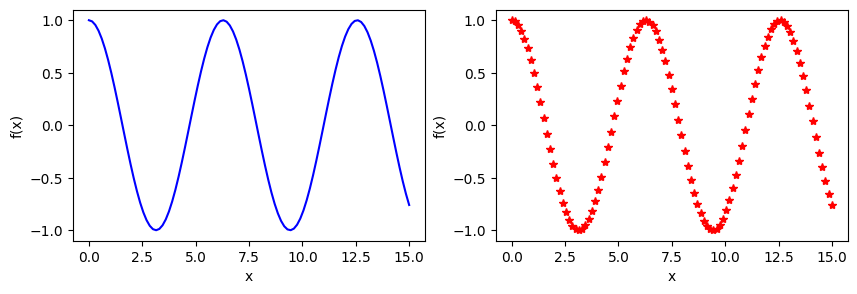
Exercise: Plot \(\cosh(x)\) and \(\sinh(x)\) in two different graphs side by side.

2.2.4. Ploting special functions

The last example plots Legendre polynomial of order 1-4.

import numpy as np
from scipy.special import legendre
import matplotlib.pyplot as plt

# define the legendre functions using scipy
l1=legendre(1)
l2=legendre(2)
l3=legendre(3)
l4=legendre(4)

#Legendre function is defined in |x|<1
x = np.linspace(-1,1,101)

# evaluate the functions
y1= l1(x)
y2= l2(x)
y3= l3(x)
y4= l4(x)

# plot all of them in the same graph with different colors
plt.figure(figsize=(6,4))
plt.plot(x,y1,'-k',label="n=1")
plt.plot(x,y2,'-b',label="n=2")
plt.plot(x,y3,'-g',label="n=3")
plt.plot(x,y4,'-r',label="n=4")

# axis labels are written as Latex equation
plt.xlabel(r"$x$")
plt.ylabel(r"$P_n(x)$")

plt.show()

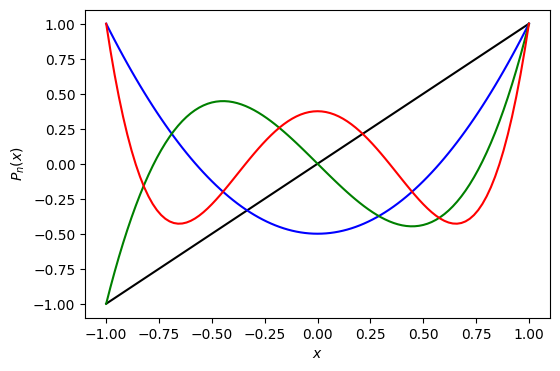
Exercise: Plot Hermite polynomials of order \(n=1,\cdots, 4\) for interval \(x = [-5,5]\).