Coupled Brownian Motors

In collaboration with:

Peter Reimann (Augsburg, Germany), Christian Van den Broeck (Limburg, Belgium), Peter Hänggi (Augsburg, Germany)


Publication

P. Reimann, R. Kawai, C. Van den Broeck, and P. Hanggi "Coupled Brownian motors: Anomalous hysteresis and zero-bias negative conductance"
Europhys. Lett. 45, (1999) 545 C. Van den Broeck, P. Reimann, R. Kawai, and P. Hänggi "Coupled Brownian Motors"
in Lecture Notes in Physics (in press, 1999)


Can we get work out of unbiased fluctuation?
It is possible for macroscopic fluctuations. However, the situation is more subtle for microscopic fluctuations. We know from the second law of thermodynamics that is is impossible to get work in a repetitive cyclic manner from a single heat bath at equilibrium. But nothing forbids the appearance of Maxwell demon in the case of nonequilibrium fluctuations. Then, it is possible to construct Brownian motors which are driven by microscopic nonequilibrium fluctuations. Such motors may be found in biological systems operating far from equilibrium.

Recently, various mathematical models of Brownian motors have been investigated. Some of them show remarkable properties such as negative mobility. In the following we introduce our own model. See References for other models.

Consider a globally coupled system of N particles with state-dependent noise (multiplicative noise):

dxi
dt
 = f(xi) + g(xi)xi + 1
N
 N
å
 j = 1 
 k(xi,xj)
where f(x), g(xi), and k(x,x¢) are deterministic force, fluctuating force, and coupling between particles, respectively. We assume that the fluctuation is represented by independent Gaussian white noises x:
< xi > = 0,        < xi(t) xj(t ¢) > = dij d(t-t ¢)
To illustrate the characteristic feature of our Brownian motor, we use the following specific model:
f(x) = - sinx - 2A sin2x
g(x) = Ö (2T+2Q (sinx + 2A sin2x)2 )
k(x,y) = K sin(x-y)
where T and Q represent strength of equilibrium and nonequilibrium fluctuations, respectively.

In order to produce flux, other models necessarily use a asymmetric potential (ratchet potential) or potential fluctuation with a finite correlation in time. Our model has neither spacial nor temporal bias but nevertheless it produces flux. How can it happen? A key point is that the system undergoes noise-induced nonequilibrium phase transition and reflection symmetry of the system is spontaneously broken. (See Figure 1 and movie) As a result the particles experiences effectively a ratchet-like potential. Figure 2 illustrates a phase diagram.

The response properties of this model is very interesting. If uniform force applied to the system in the symmetry-broken phase, anomalous hysteresis is observed (See Figure 3). Even more interestingly, if the force is applied to the system just outside the symmetry-broken region, the current flows in the opposite direction to the force. (negative zero-bias mobility, See Figure 4).

When many Brownian particles driven by multiplicative noise are coupled, many interesting phenomenon are induced through non-equilibrium phase transition and breaking of ergodicity. The coupled Brownian motor is one example. More intersting phenomenon are to be discovered.

   
Figure 1. Snapshot of a steady state.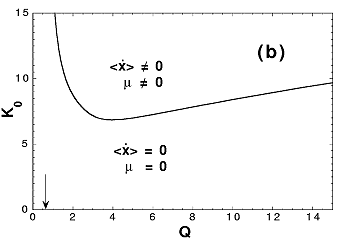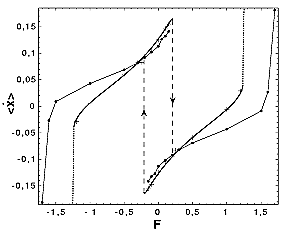
Quicktime movie(1Mb) of a steady state.


Figure 2. Phase Diagram (T=2 and A=0.15)


Figure 3. Anomalous Hysteresis Loops of the steady state current vs. force F. (T=2, A=0.15, Q=4, and K=10)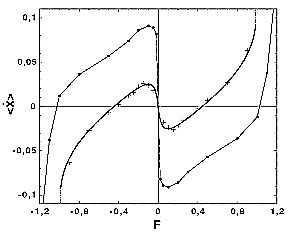


Figure 4. Negative zero-bias mobility for global(circle) and 2D nearest neighbor (plus) couplings. (Q=2 and K=8 for global coupling ans Q=6 and K=15 for 2D nearest neighbor coupling)